22. Summary
Summary
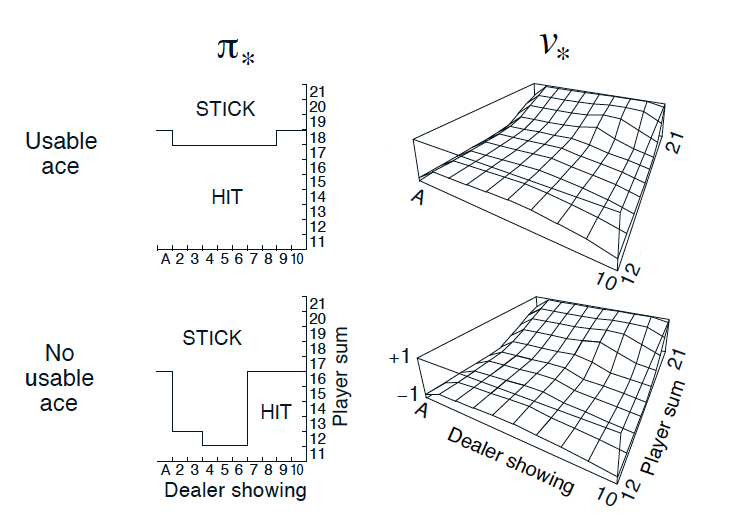
Optimal policy and state-value function in blackjack (Sutton and Barto, 2017)
## MC Prediction: State Values
- Algorithms that solve the prediction problem determine the value function v_\pi (or q_\pi) corresponding to a policy \pi.
- Methods that evaluate a policy \pi from interaction with the environment fall under one of two categories:
- On-policy methods have the agent interact with the environment by following the same policy \pi that it seeks to evaluate (or improve).
- Off-policy methods have the agent interact with the environment by following a policy b (where b\neq\pi) that is different from the policy that it seeks to evaluate (or improve).
- Each occurrence of state s\in\mathcal{S} in an episode is called a visit to s.
- There are two types of Monte Carlo (MC) prediction methods (for estimating v_\pi):
- First-visit MC estimates v_\pi(s) as the average of the returns following only first visits to s (that is, it ignores returns that are associated to later visits).
- Every-visit MC estimates v_\pi(s) as the average of the returns following all visits to s.

## MC Prediction: Action Values
- Each occurrence of the state-action pair s,a (s\in\mathcal{S},a\in\mathcal{A}) in an episode is called a visit to s,a.
- There are two types of MC prediction methods (for estimating q_\pi):
- First-visit MC estimates q_\pi(s,a) as the average of the returns following only first visits to s,a (that is, it ignores returns that are associated to later visits).
- Every-visit MC estimates q_\pi(s,a) as the average of the returns following all visits to s,a.

## Generalized Policy Iteration
- Algorithms designed to solve the control problem determine the optimal policy \pi_* from interaction with the environment.
- Generalized policy iteration (GPI) refers to the general method of using alternating rounds of policy evaluation and improvement in the search for an optimal policy, All of the reinforcement learning algorithms we examine in this course can be classified as GPI.
## MC Control: Incremental Mean
- (In this concept, we derived an algorithm that keeps a running average of a sequence of numbers.)
## MC Control: Policy Evaluation
- (In this concept, we amended the policy evaluation step to update the value function after every episode of interaction.)
## MC Control: Policy Improvement
- A policy is greedy with respect to an action-value function estimate Q if for every state s\in\mathcal{S}, it is guaranteed to select an action a\in\mathcal{A}(s) such that a = \arg\max_{a\in\mathcal{A}(s)}Q(s,a). (It is common to refer to the selected action as the greedy action.)
- A policy is \epsilon-greedy with respect to an action-value function estimate Q if for every state s\in\mathcal{S},
- with probability 1-\epsilon, the agent selects the greedy action, and
- with probability \epsilon, the agent selects an action (uniformly) at random.
## Exploration vs. Exploitation
- All reinforcement learning agents face the Exploration-Exploitation Dilemma, where they must find a way to balance the drive to behave optimally based on their current knowledge (exploitation) and the need to acquire knowledge to attain better judgment (exploration).
- In order for MC control to converge to the optimal policy, the Greedy in the Limit with Infinite Exploration (GLIE) conditions must be met:
- every state-action pair s, a (for all s\in\mathcal{S} and a\in\mathcal{A}(s)) is visited infinitely many times, and
- the policy converges to a policy that is greedy with respect to the action-value function estimate Q.

## MC Control: Constant-alpha
- (In this concept, we derived the algorithm for constant-\alpha MC control, which uses a constant step-size parameter \alpha.)
- The step-size parameter \alpha must satisfy 0 < \alpha \leq 1. Higher values of \alpha will result in faster learning, but values of \alpha that are too high can prevent MC control from converging to \pi_*.
